Chaotic Attractors

April 2023

See code

Rust

macroquad

egui

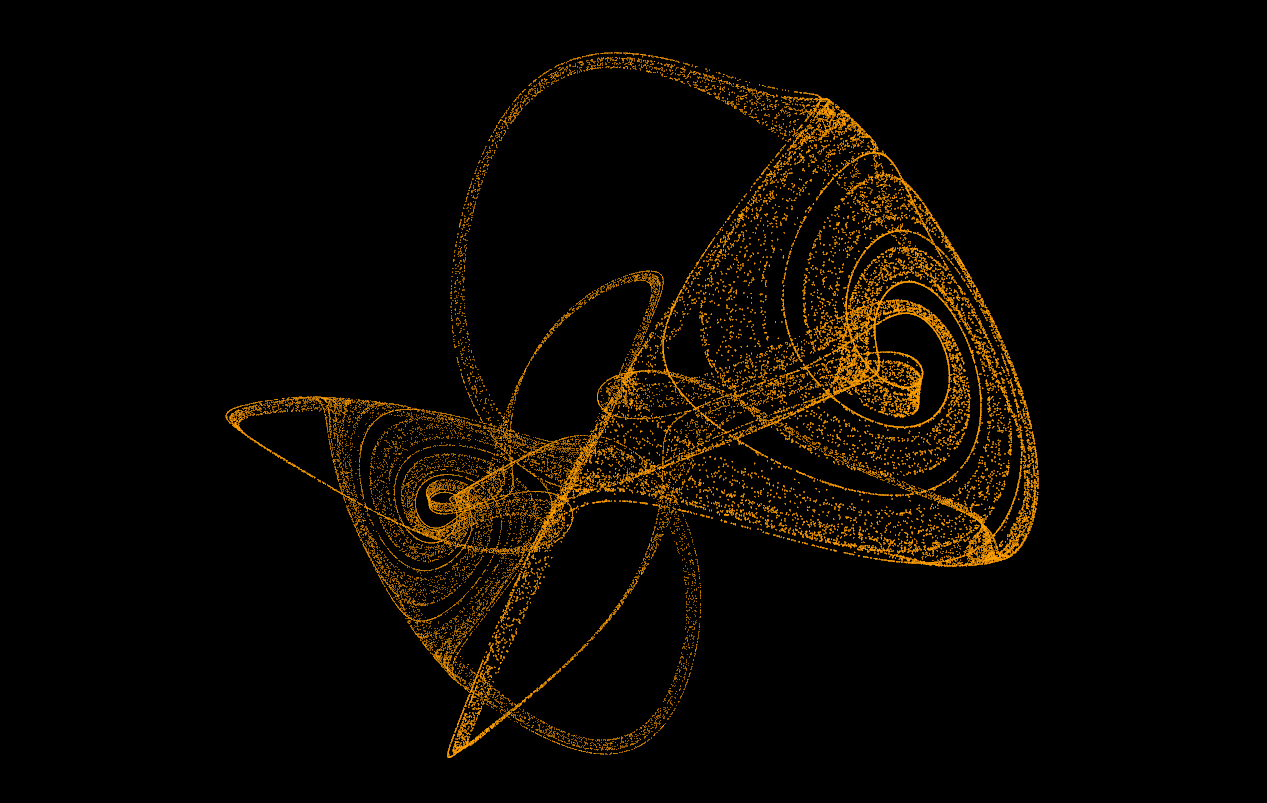
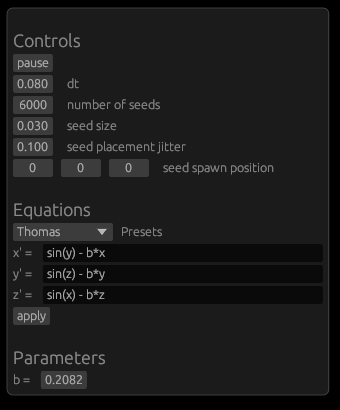
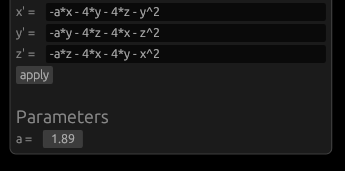
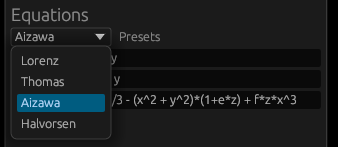
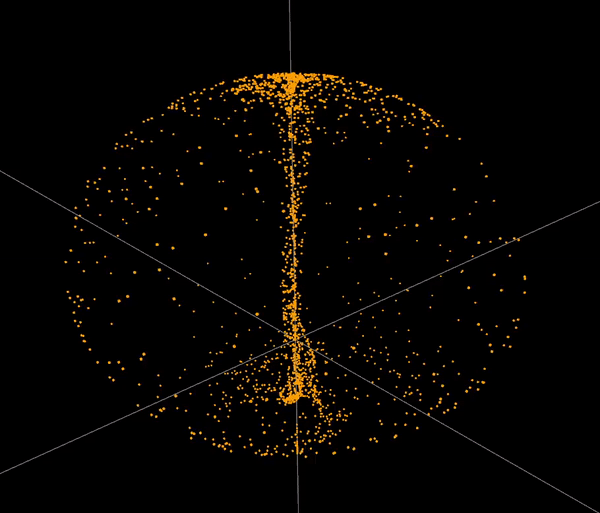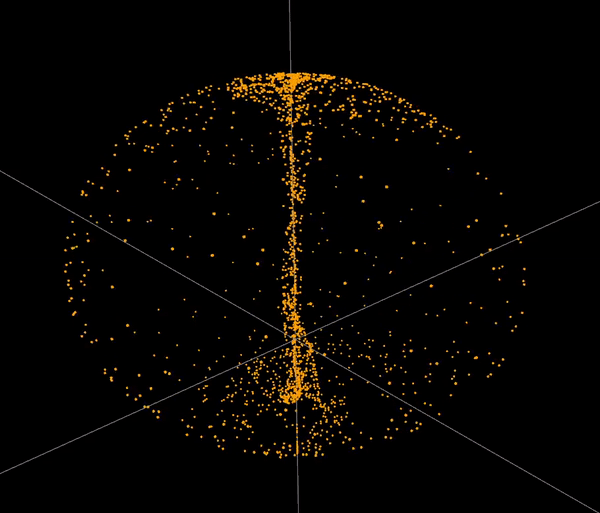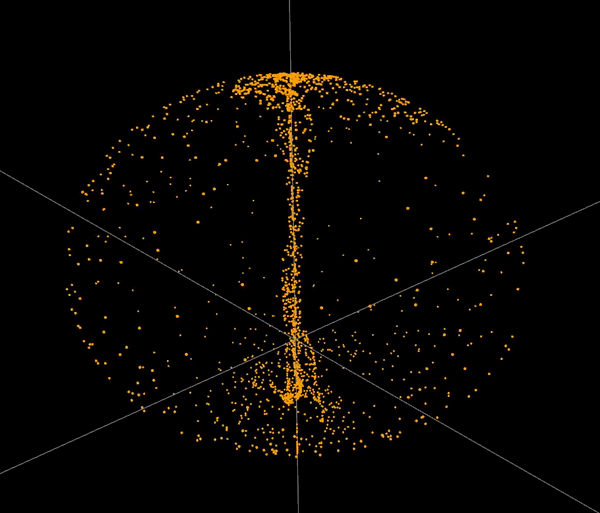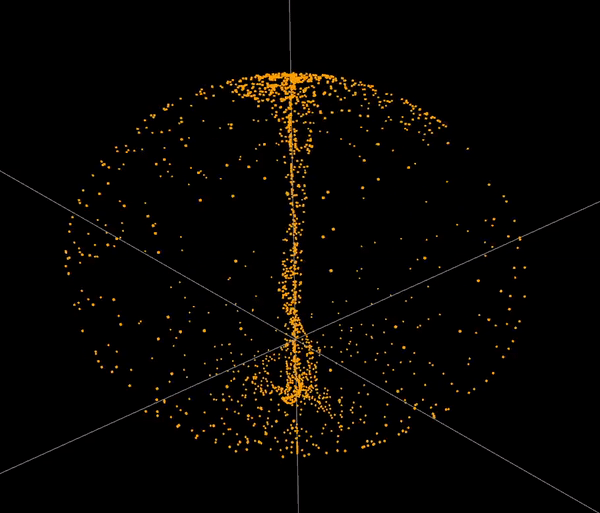
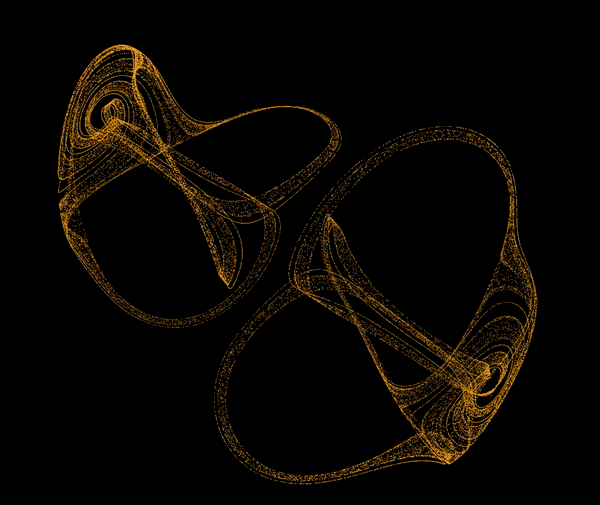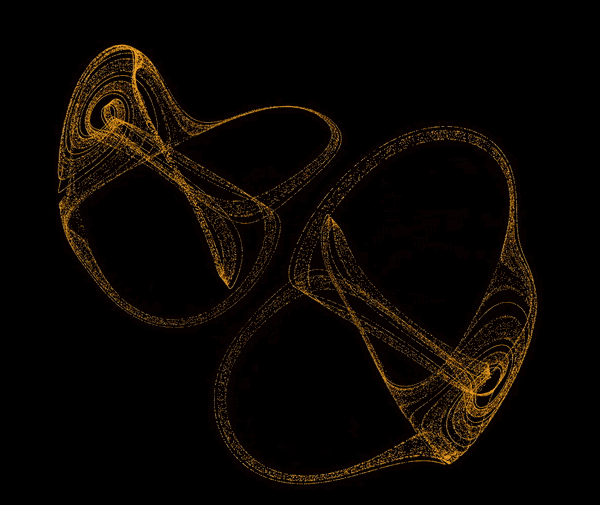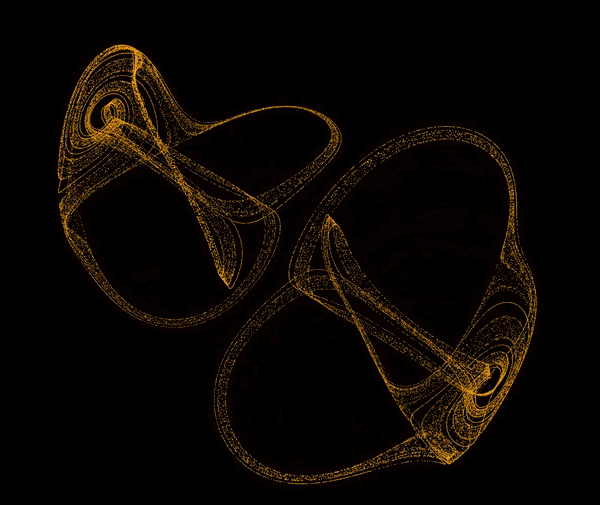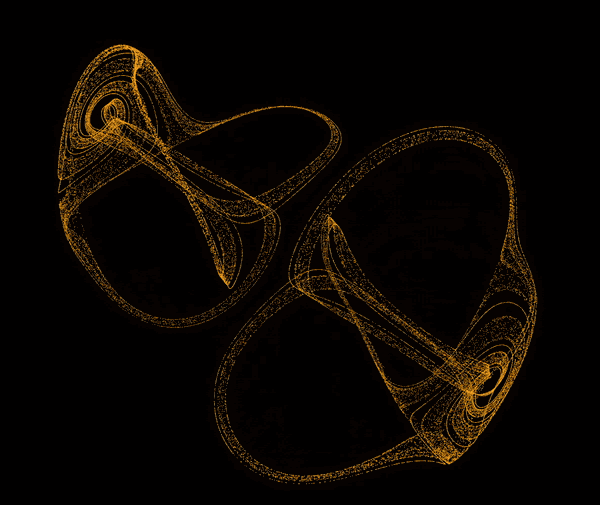The software simulates chaotic attractors, which are mathematical objects that have a tendency to converge to a certain set of points. The user can choose from a set of predefined attractors, or define their own. To define an attractor the user has to provide a system of differential equations. The software then tokenizes the equations and turns them into three abstract syntax trees. The trees are then used to to simulate point paths and to display the attractor. The user can also modify the parameters of the simulation. The software is capable of simulating and displaying ~60 000 points at comfortable framerate.

arrow_back_ios

arrow_forward_ios

close